Quick Recap: Precision and recall are technical metrics: precision is "of results returned, how many are correct?" recall is "of all correct results, how many did we find?" But in financial operations, these metrics translate directly to business risk. High recall but low precision in fraud detection means catching fraud but also flagging legitimate transactions (customer frustration, operational cost). Low recall but high precision means missing real fraud (financial loss). Understanding the business risk behind each metric choice is critical for making governance-acceptable trade-offs.
It's Monday morning at a bank's fraud team. They're deciding: should their fraud detection system catch 99% of fraud (high recall) or avoid false positives (high precision)?
Option A: High Recall (99% fraud caught, 5% false positives)
Catches 990 of 1,000 fraudulent transactions
Also flags 950 legitimate transactions as suspicious
Customer experience: "My card got declined 5 times this week. I'm switching banks."
Operational cost: 950 false alerts that investigators must review (1 hour each = 950 labor hours/week)
Annual cost of false positives: ~$2M in investigator time
Option B: High Precision (95% fraud caught, 0.5% false positives)
Catches 950 of 1,000 fraudulent transactions
Flags only 95 legitimate transactions as suspicious
Customer experience: "My card works fine"
Operational cost: 95 false alerts (95 labor hours/week = $500K/year)
BUT: 50 fraudulent transactions slip through (losses: $500K-$2M depending on fraud amount)
The bank chooses Option B. High precision, accept 50 frauds slipping through, because the operational cost of high recall is higher than the loss from missed fraud.
This trade-off—between precision, recall, and actual business risk—is what regulators want to see. Not just "our model has 95% accuracy," but "we chose precision over recall because the operational cost of false positives exceeded the risk of missed fraud."
Metrics vs. Business Risk
Precision: Of results returned, how many are correct?
Formula: True Positives / (True Positives + False Positives)
Range: 0% to 100%
Example: System flags 100 transactions as fraud. 95 are real fraud, 5 are legitimate. Precision = 95%
Recall: Of all correct results, how many did we find?
Formula: True Positives / (True Positives + False Negatives)
Range: 0% to 100%
Example: 1,000 fraudulent transactions occurred. System caught 950. Recall = 95%
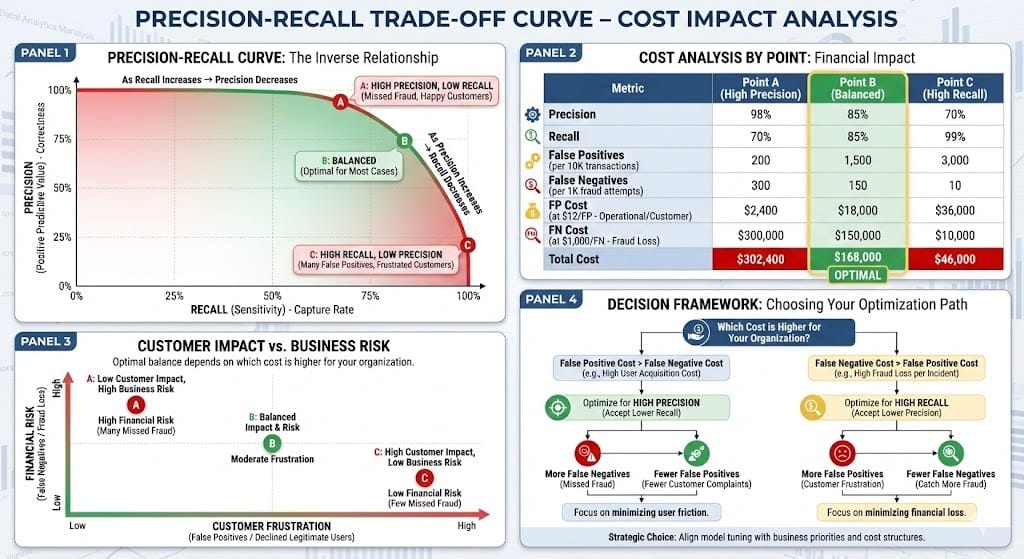
The Trade-off: Improving one typically hurts the other.
How: Lower the fraud detection threshold (catch more fraud, improve recall from 95% to 99%). But now you also catch more legitimate transactions (precision drops from 95% to 90%).
Why: You're accepting lower precision to get higher recall. You're catching more fraud, but also more false positives.
Business Risk Behind Each Metric:
Precision Risk: False positives have costs.
Fraud detection: Customer frustration, card declines, churn
Compliance search: Investigators waste time on irrelevant documents
Loan approval: Deny good applicants, opportunity cost
Each false positive has a cost (customer time, investigator time, lost revenue)
Recall Risk: False negatives have costs.
Fraud detection: Fraudsters slip through, financial loss
Compliance search: Miss relevant documents, regulatory violation
Loan approval: Approve risky applicants, loan loss
Each false negative has a cost (fraud loss, regulatory fine, credit loss)
The decision: Optimize for whichever cost is higher.
Deep Dive: Quantifying Business Risk for Trade-offs (2026)
Framework: Cost-Benefit Analysis for Precision vs. Recall
Step 1: Calculate Cost of False Positive
What does it cost your organization when the system incorrectly flags a legitimate item?
Fraud Detection Example:
False positive: System flags legitimate transaction as fraud
Cost elements:
Customer service call to verify: $5 (staff time)
Customer frustration: 1% probability of churn (0.01 × $500 annual customer value = $5)
Operational review: $2 (investigator time to review and clear)
Total false positive cost: $12 per false positive
Compliance Search Example:
False positive: System returns irrelevant document for compliance search
Cost elements:
Investigator reviews wrong document: $8 (30 min at $16/hour)
Total false positive cost: $8 per false positive
Loan Approval Example:
False positive: System recommends denial of good applicant
Cost elements:
Lost revenue from good applicant: $500-$2,000 (over loan lifetime)
Regulatory risk if pattern emerges: minimal (one applicant)
Total false positive cost: $500-$2,000 per false positive
Step 2: Calculate Cost of False Negative
What does it cost when the system misses something it should have caught?
Fraud Detection Example:
False negative: System misses fraudulent transaction
Cost elements:
Direct fraud loss: $500-$10,000 (transaction amount)
Chargeback cost: $50 (processing fee)
Investigation time: $5 (if caught later)
Total false negative cost: $555-$10,050 per false negative
Compliance Search Example:
False negative: System misses relevant compliance document
Cost elements:
Regulatory violation: $1M-$10M (fine for inadequate investigation)
Reputational damage: $5M-$50M (estimated)
Total false negative cost: $6M-$60M per false negative
Loan Approval Example:
False negative: System misses risky applicant, loan defaults
Cost elements:
Loan loss: $50,000-$500,000 (depending on loan size)
Regulatory cost if pattern emerges: $1M-$10M
Total false negative cost: $51M-$510M per false negative
Step 3: Calculate Optimal Precision/Recall Balance
Formula: Find threshold that minimizes: (False Positives × Cost_FP) + (False Negatives × Cost_FN)
Fraud Detection Example:
Cost of FP: $12
Cost of FN: $1,000
Current system: 99% recall, 90% precision
On 10,000 legitimate transactions: 1,000 false positives = $12,000 cost
On 1,000 fraudulent transactions: 10 false negatives = $10,000 cost
Total cost: $22,000
Alternative: 95% recall, 98% precision
On 10,000 legitimate transactions: 200 false positives = $2,400 cost
On 1,000 fraudulent transactions: 50 false negatives = $50,000 cost
Total cost: $52,400 (worse)
Better alternative: 97% recall, 95% precision
On 10,000 legitimate transactions: 526 false positives = $6,312 cost
On 1,000 fraudulent transactions: 30 false negatives = $30,000 cost
Total cost: $36,312 (better than 99% recall)
Decision: Adjust threshold to achieve 97% recall, 95% precision. Minimize total cost.
Real-World Complexity: Multi-Stage Systems
In practice, financial systems are multi-stage. Precision and recall decisions at each stage compound.
Example: Loan Approval Pipeline
Stage 1: Initial Screening (Automated)
Goal: Filter obvious rejections quickly
Optimize for: High recall (don't miss good applicants)
Accept: Lower precision (some bad applicants pass to stage 2)
Recall: 98%, Precision: 70%
Rationale: False negatives (rejecting good applicants) are very costly. False positives get human review anyway.
Stage 2: Risk Assessment (Automated)
Goal: Score remaining applicants
Optimize for: Balanced precision/recall
Accept: Moderate false positives and negatives
Recall: 90%, Precision: 85%
Rationale: Need balance because both errors are costly. Some flagged applicants go to stage 3, some are approved
Stage 3: Human Review (Manual)
Goal: Final decision on flagged cases
Optimize for: High precision on human-reviewed cases
Accept: All applicants here have already been filtered (stage 1 recall = 98%)
Recall: 95%, Precision: 98%
Rationale: Humans are expensive but accurate. They catch what automation missed or was uncertain about
Overall System Metrics:
Final recall: 98% × 90% × 95% = 83.8% (applications that should be approved are approved)
Final precision: Harder to calculate (depends on how stages interact), ~85-90%
Key insight: Each stage optimizes for different goals. Early stages prioritize recall (don't filter good customers). Late stages prioritize precision (humans are expensive).
2026 Regulatory Perspective
Federal Reserve Guidance (2025-2026):
Banks must document precision/recall trade-offs
Decision must be justified by cost analysis
Both false positives and false negatives must be monitored
If trade-off changes (e.g., fraud losses increase), system must be re-optimized
EBA Guidance (2026):
Fairness requirements complicate precision/recall optimization
Can't optimize for precision if it means disproportionately hurting minority applicants
Must achieve acceptable precision/recall while maintaining fairness across demographics
Practical implication (2026): Optimization must satisfy three constraints:
Business cost (precision/recall trade-off)
Fairness (equal treatment across demographics)
Regulatory acceptable thresholds (minimum precision/recall)
These can conflict, requiring careful navigation.

BFSI-Specific Patterns
Pattern 1: Risk-Segmented Thresholds
Different products have different precision/recall requirements:
High-value loans ($1M+): Optimize for precision (better to deny good applicant than approve bad one)
Small loans (<$50K): Optimize for recall (better to catch fraud than perfect accuracy)
Credit cards: Optimize for recall (fraud cost >> false positive customer frustration)
Each product has its own optimal threshold.
Pattern 2: Seasonal Re-optimization
Precision/recall thresholds change seasonally or when fraud patterns change:
Q4 (holiday season): Fraud increases 3-5x. Lower precision threshold to catch more.
Post-pandemic (2024-2026): Fraud patterns shifted. Reoptimize.
Annual audit at minimum; quarterly when markets shift.
Pattern 3: Fairness-Constrained Optimization
Can't optimize precision/recall if it hurts fairness:
Your optimal precision point has 10% approval rate disparity (men vs. women)
Regulatory requirement: <5% disparity
Accept suboptimal precision/recall if needed to meet fairness constraint
Multi-objective optimization: minimize cost AND meet fairness constraints.
Looking Ahead: 2027-2030
2027: Dynamic Thresholding
Precision/recall thresholds automatically adjust based on:
Current fraud rates (higher fraud → lower precision threshold)
Customer churn rates (high churn → lower false positive threshold)
Regulatory changes (new fairness requirements → adjust thresholds)
2028: Real-Time Cost Recalculation
Cost of false positives and negatives changes in real-time:
False positive cost increases during customer service outages (more complaints)
False negative cost increases during fraud waves
System automatically reoptimizes thresholds hourly
2029: Fairness-Aware Precision/Recall
New metrics that optimize precision/recall while maintaining fairness:
"Fair precision" (precision within each demographic group)
"Fair recall" (recall within each demographic group)
Threshold optimization considers both accuracy AND fairness
HIVE Summary
Key takeaways:
Precision and recall are technical metrics, but they translate directly to business costs: false positives have operational costs, false negatives have financial costs. Optimal threshold minimizes total cost, not maximizes accuracy
Cost analysis framework: quantify cost per false positive, cost per false negative, then find threshold that minimizes (FP × Cost_FP) + (FN × Cost_FN). This is how regulators expect decisions to be justified
Multi-stage systems (automated screening → risk assessment → human review) can have different precision/recall optimizations at each stage. Early stages optimize for recall, late stages for precision
2026 regulatory baseline: Precision/recall trade-offs must be documented, cost-justified, and re-optimized when fraud rates, customer churn, or fairness constraints change
Start here:
If deploying ML systems: Don't just optimize for accuracy. Calculate costs of false positives and negatives for your specific use case. Use cost analysis to justify your precision/recall choice
If facing regulatory pressure on FP or FN rates: Run cost analysis. Show regulators that your chosen threshold minimizes total business cost while meeting fairness constraints
If noticing patterns in false positives/negatives: Check if costs have changed (fraud increased? customer churn higher?). If so, re-optimize thresholds quarterly
Looking ahead (2027-2030):
Dynamic thresholding will adjust precision/recall automatically based on real-time costs and fraud rates
Real-time cost recalculation will optimize thresholds hourly as business conditions change
Fairness-aware precision/recall metrics will emerge to optimize for both accuracy and equal treatment
Open questions:
How do we estimate costs of false positives accurately? Customer churn is hard to predict from single false positive
When regulatory constraints conflict with cost optimization, which takes priority?
Can we predict future fraud costs to optimize proactively rather than reactively?
Jargon Buster
Precision: Of items flagged by system, how many are correct? "95% precision" means 95 of 100 flagged items are true positives, 5 are false positives. Why it matters in BFSI: Lower precision = more false positives = customer frustration, operational cost. High precision = fewer false positives = customers happy, but more fraud slips through
Recall: Of all true items, how many did system find? "95% recall" means system found 95 of 100 true fraud cases, missed 5. Why it matters in BFSI: Lower recall = more missed fraud = financial loss. Higher recall = catch more fraud, but also more false positives. Trade-off between the two
False Positive: System flags item incorrectly (legitimate transaction flagged as fraud, good applicant rejected). Why it matters in BFSI: False positives have customer-facing costs (frustration, churn, operational review cost). Must balance against false negatives
False Negative: System misses item (fraudulent transaction not flagged, risky applicant approved). Why it matters in BFSI: False negatives have financial costs (fraud loss, loan defaults). Must balance against false positives
Precision-Recall Trade-off: Improving one typically worsens the other. Lower threshold catches more items (higher recall, lower precision). Higher threshold catches fewer, higher-confidence items (lower recall, higher precision). Why it matters in BFSI: Must choose threshold that minimizes total business cost (FP cost + FN cost)
Cost-Benefit Analysis: Quantifying cost of false positives and negatives, then optimizing threshold to minimize total cost. Why it matters in BFSI: Regulators expect decisions to be cost-justified, not just accuracy-optimized
Multi-Stage System: Pipeline with multiple decision stages (screening → assessment → review). Each stage can have different precision/recall optimization. Why it matters in BFSI: Allows early stages to prioritize recall (don't filter good customers) and late stages to prioritize precision (expensive human review)
Threshold: Decision boundary that determines what gets flagged. Lower threshold = higher recall, lower precision. Higher threshold = lower recall, higher precision. Why it matters in BFSI: Choosing the right threshold is critical. Same model, different threshold = completely different business outcomes
Fun Facts
On Cost Analysis Surprises: A bank thought their fraud detection should maximize recall (catch all fraud). Cost analysis revealed false positives cost $12 each, fraud losses cost $1,000 each. With 10K legitimate and 1K fraudulent transactions, 99% recall (10 missed frauds, 500 false positives) cost $11,000 total. 95% recall (50 missed frauds, 100 false positives) cost $51,200 (worse). 97% recall (30 missed frauds, 300 false positives) cost $330K (better balance). They discovered 97% recall was actually optimal, not 99%. Lesson: Don't assume you want maximum recall. Cost analysis reveals true optimum
On Fairness-Constrained Optimization: A bank optimized loan approval for lowest total cost. Optimal precision was 88%, but this created 12% approval rate disparity (men vs. women). Regulatory requirement: <5% disparity. They had to accept 82% precision (lower cost efficiency, but fair). Lesson: Fairness constraints override pure cost optimization. Must multi-objective optimize
For Further Reading
Precision, Recall, and ROC Curves for Financial ML (O'Reilly, 2025) | https://www.oreilly.com/library/view/precision-recall-financial/9781098162839/ | Guide to understanding trade-offs with real financial examples. How to quantify costs, optimize thresholds.
Cost-Based Threshold Optimization for Banking (Journal of Financial Technology, 2025) | https://arxiv.org/abs/2501.11234 | Research on cost-benefit analysis for precision/recall. Frameworks for quantifying false positive and negative costs.
Multi-Stage Decision Systems in Financial Services (Risk Management Institute, 2025) | https://www.rmins.org/research/multi-stage-decisions | How banks structure screening → assessment → review pipelines. Precision/recall optimization at each stage.
Fairness-Accuracy Trade-offs in Regulated Lending (Federal Reserve, 2025) | https://www.federalreserve.gov/newsevents/pressreleases/files/bcreg20250120a.pdf | Regulatory expectations for balancing accuracy with fairness. When to sacrifice precision/recall for equity.
Threshold Optimization Case Studies 2024-2026 (ABA Financial Services, 2025) | https://www.aba.com/research/thresholds-2025 | Real examples of banks optimizing thresholds. Lessons from fraud detection, lending, compliance.
Next up: Internal RAG Search Console UI — Provide safe internal search and decision-support for teams
This is part of our ongoing work understanding AI deployment in financial systems. If you're optimizing precision/recall thresholds, share your approaches for cost quantification, multi-stage optimization, or fairness-constrained threshold selection.
